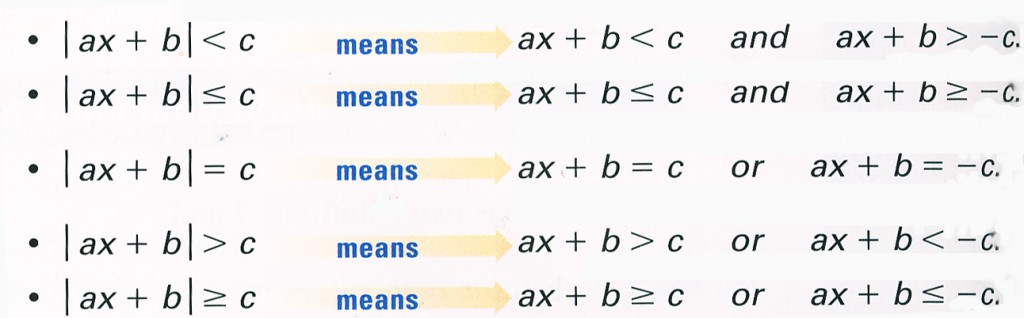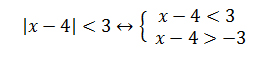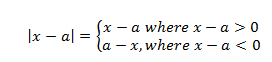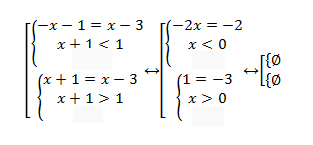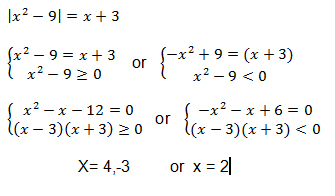Definition and properties absolute value
For any Real number the absolute value or modulus of a is denoted by |a| and is defined as:
As can be seen from the above definition, the absolute value of a is always either positive or zero, but never negative.
From an analitic geometry point of view, the absolute value of a real number
is that number’s distance from zero along the real number line, and more generally the absolute value of the difference of two real numbers is the distance between them.
For example, |-5| = 5. It is mean that distance from point -5 to zero equal 5.
Let’s look on simple equation: |x| = 3. We can see, that on graph there are two points with distance equal 3 to the zero. These are points 3 and -3. So equation |x| = 3 has a two solutions: x = 3 and x = -3.
Example 1
|x — 3| = 4.
This equation you can read as: The distance from point x to the point 3 is equal 4. Using a graph we can find the two solutions for this equation.
These are points -1 and -7
Example 2
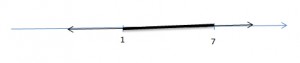
Let’s solve inequality: |x + 7| < 4.
You can read it as: the distance from point x to the point -7 less than 4.
Answer: (-11; -3).
Example 3
Let’s solve inequality: |10 — x| ≥ 7.
Or you can interpret it like as distance from point 10 to the point x is greater than 7
Answer: (-∞; 3] and [17, +∞)
The absolute value has the following seven fundamental properties:
1. Modules of opposite numbers are equal:
2. Square of the modulus equal to the square of the number:
3. Square root of the square number is module of this number :
4. The module of the number is non-negative number:
5. Constant positive factor can be taken out of the module sign:
6. If , then
.
7. Module is the product of two (or more) numbers is equal to the product of their modules:
Let’s consider the solution of inequalities with module. Each absolute -value equation or inequality is rewitten as two equations or two inequalities joined by “and” or “or”.
Notice that when an absolute value is less than a number, the inequalities are connected by “and”. When an absolute value is greater than a number, the inequalities are connected by “or”.
Example 4
x < 7 and x > 1
Example 5
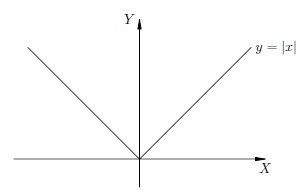
Graph function of modulus
The general approach is when we are solving the unequality or equality with module, the basic method is to opening the sign of the module according to its properties.
Thus, if the modulus is an expression depended on the variable, we are opening module following the definition of module:
Example 6
Solve equaltion:
For this type of equation we can not use the method we used above because right part of have a variable, for this case we gave to use general approach :
Let’s open the module sign:
So, we have no solution for this equation.
Example 7
Solve equaltion:
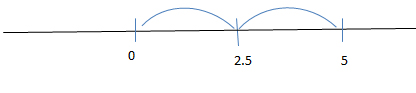
Example 8
Let’s find the point equidistant from points 0 and 5.
So solution will be x = 2.5
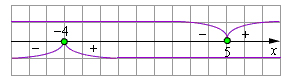
Another most common method for solving equations with module are calling as method of the intervals. The main idea of this approach is division all domain into intervals with ends where a modules are become equal zero.
Example 9
The expression under the sign of absolute value, are zero at x = -4 and x = 5. So, we need to consider three intervals:
1) x ≤ –4;
2) –4 < x ≤ 5;
3) x > 5.
The figure shows the sign will be before each module on each of the three periods:
- x ≤ –4. In this case: 2x + 8 < 0, x – 5 < 0. So on this interval equation become
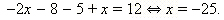
- –4 < x ≤ 5; the equation become:
- x > 5 the equation become:
In this case we can see that solution x= -1 is not belong to the interval x>5. x=-1 is not a solution.
So answer would be just two points : -25 and -1.