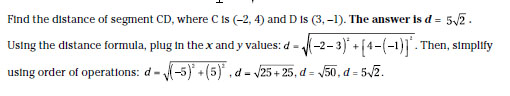These functions are known as “linear” because they are precisely the functions whose graph is a straight line.
Such a function can be written as:
f(x) = mx + b ,
where m is a slope.
The slope of a nonvertical line is the ratio of vertical changer (the rise) to horizontal change (the run). Just as two points determine a line, two points are all that are needed to determine a line’s slope. The slope of line is same regardless of which two points are used.
The slope of the nonvertical line passing through the points (x1,y1) and (x2,y2) is :
Slope-intercept form. Given the slope m and the y-intercept b, use this equation:
Point – slope form Given the slope m and a point (x1,y1) , use this equation:
Two points Given two points (x1,y1) and (x2,y2), use the formula:
To find the slope m. Then use the point –slope form with this slope and either of the given point to write an equation of the line.
Standard form
The standard form for the equation of a line is written Ax+By =C
One example of such a line is 4x+3y =12
The standard form has more information than may be immediately apparent. You can determine, just by looking at the numbers in the equation, the intercepts and slope of the line. The line
Ax+By = C has
Classification of lines by slope
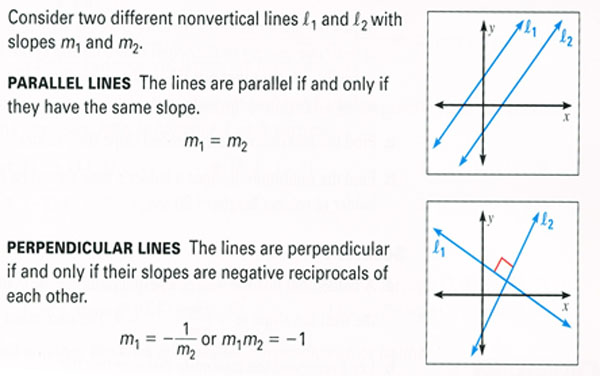
Slopes of Parallel and perpendicular lines
Example 1
The lines with equations x + 3y = 2 and -2x + ky = 5 are perpendicular for k =
A) -3
B) -2
C) -1
D) 0
E) 2/3
Solution
The line with equations x + 3y = 2 has slope -1/3 so following the perpendicular condition the slope perpendicular line has to be negative reciprocal so equal 3. In general case the slope line -2x + ky = 5 equal 2/k and we need it become equal 3. So k =3/2 ,that is mean right answer is E)
Using graphs to find information (distance, midpoint)
Graphs are more than just pretty pictures. From a graph, it’s possible to determine two points. From these points, you can determine the distance between them, the midpoint of the segment connecting them, and the slope of the line connecting them.
Finding the distance
Distance is how far two things are apart. In this case, you’re finding the distance between two parts. Knowing how to calculate distance is helpful for when you get to conics. To find the distance between two points (x1,y1) and (x2,y2), you can use the following formula:
Calculating the midpoint
The midpoint as you would think is the middle of a segment. To find the midpoint of those same two points (x1,y1) and (x2,y2) you just need to average the x and values and express them as an order pair:
Example 2
Find the distance of segment CD, where C is (–2, 4) and D is (3, –1).
Solution