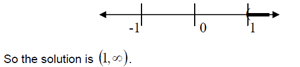The notation a ≠ b means that a is not equal to b.
The notation a < b means that a is less than b.
The notation a > b means that a is greater than b.
In either case, a is not equal to b. These relations are known as strict inequalities. The notation a < b may also be read as “a is strictly lesser than b”.
In contrast to strict inequalities, there are two types of inequality relations that are not strict:
The notation a ≤ b means that a is less than or equal to b (or, equivalently, not greater than b, or at most b).
The notation a ≥ b means that a is greater than or equal to b (or, equivalently, not less than b, or at least b)
In order to simplify matters we want to define a new type of notation for inequalities.
Example 1
Solve and graph. Put your answer in interval notation.
-2x + 3 < 1
Solution:
So we can simply solve this inequality as we solved equations. We just isolate the x on one side. The only thing we have to remember is that when we have to divide by a negative, we will need to “flip” the inequality symbol. We proceed as follows:
-2x + 3 < 1
-2x < 1 – 3
-2x < -2
x > 1
Now we simply graph and write the answer in interval notation:
Second degree of inequality in the general form is written as follows:
ax2 + bx + c > 0 or ax2 + bx + c < 0 and a ≠0
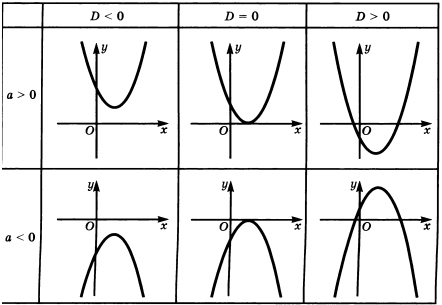
Solution of the inequality of the second degree is to find intervals in which the quadratic function is positive or negative.
The figure above shows the graph of the quadratic unction depending on the value of the discriminant D = b2-4ac
Example 2
Solve inequality:
2x2 – 5x + 2 <0
Solution
First let’s calculate discriminant : D = 25-4*2*2=9 >0
So our 2x2 – 5x + 2 = 0 has two solutions, fist x1= 1/2, second x2= 2.
Because a >0, parabola open up and solution our inequity will be interval between these roots:
( ½ ; 2)
Inequalities with one variable third or higher degree can sometimes be solved by using a special method,called as the method of intervals.
The first step in solving a polynomial inequality is to find the polynomial’s zeros (its x-intercepts). Between any two consecutive zeros, the polynomial will be either positive or negative. Since the inequality is asking for positivity (“greater than zero”) or negativity (“less than zero”), finding the intercepts (“equal to zero”) is the way to get started. If you think of the problem graphically, the zeros are where the polynomial crosses the x-axis; between any two consecutive crossing-points, the polynomial will either be above the axis (and thus positive) or below it (and thus negative).
Let’s take function f(x) = (x+4)(x-3)(x-8)
Domain of this function is (-∞;+∞)
Let’s mark zeros and will check sign on each interval:
So we see that signs alternate.