We use the following symbol 
to indicate congruence: It means not only are the two figures the same shape (~), but they have the same size (=).
It is important to recognize that in a congruent triangle, each part of it is also obviously congruent. If two triangles are congruent, then naturally all the sides are angles are also congruent with their corresponding pair.
In every congruent triangle:
(1) there are 3 sets of congruent sides and
(2) there are 3 sets of congruent angles.
If we need to prove that two triangles are congruent, we have four different methods:
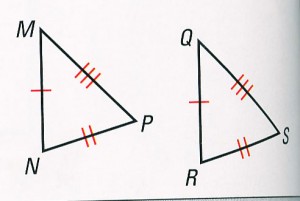
1. SSS (side side side) = If three sides of one triangle are congruent to three sides of another triangle, the triangles are congruent.
∆ MNP ∆ RQS
2. SAS (side angle side) = If two sides and the angle in between are congruent to the corresponding parts of another triangle, the triangles are congruent.
∆ PQS ∆ WXY
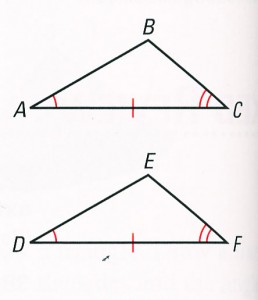
3. ASA (angle side angle) = If two angles and the side in between are congruent to the corresponding parts of another triangle, the triangles are congruent.
∆ ABC ∆ DEF
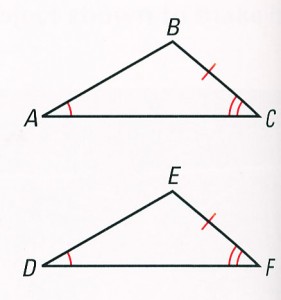
4. AAS (angle angle side) = If two angles and the non-included side of one triangle are congruent to the corresponding parts of another triangle, the triangles are congruent.
∆ ABC ∆ DEF
But let’s look at most common mistakes when we make deal with congruent triangles.
Is triangle ABC congruent to triangle XYZ?
What do we know from this picture? We see an angle and two sides that are congruent. However, there is no congruence for Angle Side Side. Therefore we can’t prove that the triangles are congruent.
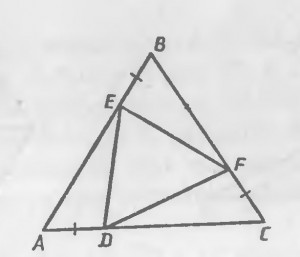
Problem 1
Given: BD EC, AC AD
Prove: AB AE
Solution
From BD EC, AC AD ⤇ ∆CAD – isosceles, then ⦟ACD = ⦟ADC ⤇ ⦟BCA = ⦟ADE ⤇ ∆ ABC ∆ ADE (SAS) ⤇ AB AE.
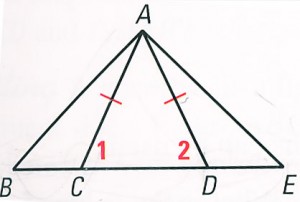
Problem 2
Given: ∆ ABC equilateral and EB FC AD
Prove: ∆ EDF – equilateral
Solution
1. Because ∆ ABC equilateral ⤇ AB BC AC, then if we will subtract from each equal side the same length segment EB FC AD we will get the same
lenght segments, so AB – EB BC – FC AC – AD ⤇ AE BF CD.
2. Because ∆ ABC equilateral ⤇ ⦟A = ⦟B = ⦟C.
So from (1),(2) and EB FC AD ⤇ (using SAS theorem) ∆ ADE ∆ EBF ∆ DFC ⤇ ED EF FD, so ∆ EDF- equilateral.
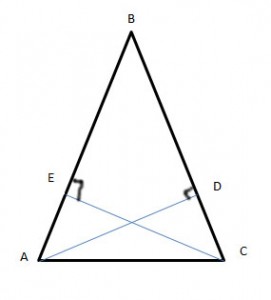
Problem 3
Given: EC DA – altitudes.
Prove: ∆ ABC – isosceles
Solution
Let’s prove that ∆ ABD ∆ CEB, notice that both are right triangles, EC DA (given) , ⦟B – common, so (using theorem AAS) ∆ ABD ∆ CEB.
So because ∆ ABD ∆ CEB its hypotenuses are equal too,so AB BC it is mean that ∆ ABC – isosceles.
