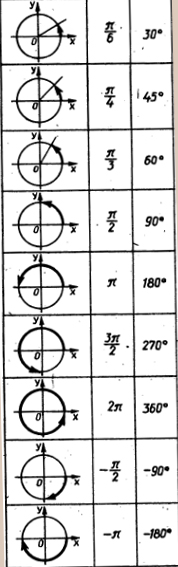
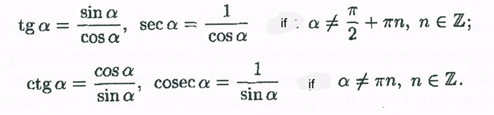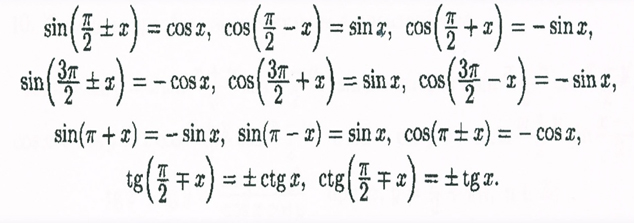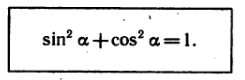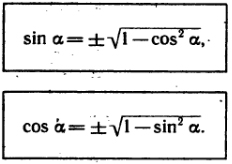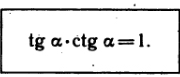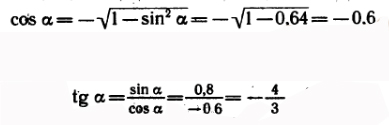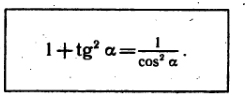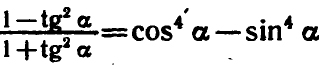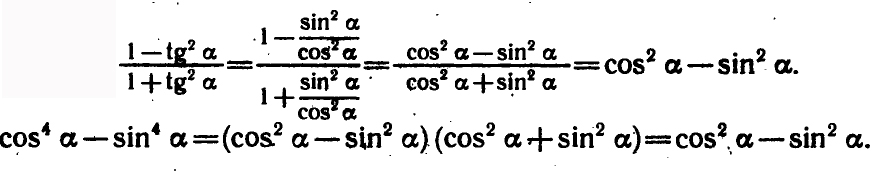Consider Figure 1 which shows a circle of radius 1 unit centered at the origin. Imagine a point M on the circle which moves around the circle in an anticlockwise sense. Figure 1 angles measured anticlockwise from the positive X axis are deemed to be positive angles.
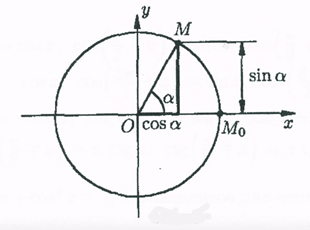
Figure 1
In the first diagram in Figure 1 the angle is acute, that is, it is greater than 0◦ but less than 90◦(π/2) . When M moves into the second quadrant, the angle lies between 90◦(π/2) and 180◦(π). The angle is now obtuse. When M moves into the third quadrant, the angle is greater than 180◦(π) but less than 270◦(3π/2). Finally in the fourth quadrant, the angle is greater than 270◦ (3π/2) but less that 360◦.On these diagrams the arm OM is moving in a clockwise sense from the positive x axis. Such angles are conventionally taken to be negative angles. Sin(α) will be projection of OM onto the y axis and Cos(α) will be projection of OM onto the X axis.
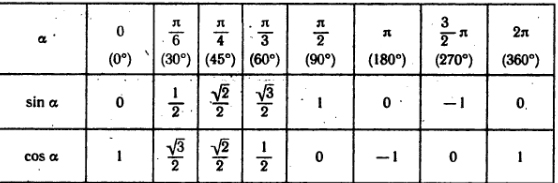
Here is a table of some angle turns expressed in degrees and radian measures.
The whole pattern of Sin(α) and and Cos(α) is reproduced every 360◦. In this way we can find the sine of any
angle at all.
Now using all this information we can easy memories the formulas of Even/Odd Identities:
We just need imagine every times in which quadrant will be our imaginary point and where we are making projection.
Almost the same approach we are using for the formulas when we add or subtract π/2 only need to memories that when we add or subtract π/2 we have to change cos on sin, sin on cos, tan on cot. And every times we have check the sing of the function.
Example 1
Simplify: Sin(x+π/2)
Solution
So we see π/2 so the Sin will change on Cos then angle x+π/2 correspond to the second quadrant, the projection to the Y axis is positive, so we can make conclusion that Sin(x+π/2) = Cos(x) .
Thinking similarly way we could prove the next ones:
Here is a Sin and Cos table for the most common angle values:
Example 2
Solve equation : Cos (5 π/2+x) = -1
Solution:
Let’s simplify left part first: Cos (5 π/2+x) = Cos (2π+ π/2+x) = Cos ( π/2+x) =- Sin (x).
Now we need solve equation: Sin(x) =-1 , so x = 3π/2 +2πk, k – whole number.
Let’s find out the relationship between the functions of Cos and Sin, Tan and Cot.
If we will call back to Fig.1 , using the Pythagorean Identities we can get it’s analog for the trigonometry:
or if express functions Sin or Cos we can get:
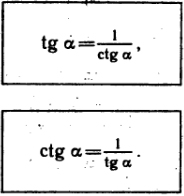
Dependence of functions Tan and Cot can be expressed by following :
or :
Example 3
Calculate tan α if Sin (α) = 0.8 and
Solution
First of all notice, that Cos(α) < 0 because α is on second quadrant. So using upper formula we will get:
If Pythagorean Identities divided by 
and evaluate it we can get another important identities :
Example 4
Prove that:
Solution:
